Рассмотрим в качестве примера балансовую воспроизводственную матрицу «производства и потребления» некого условного общества, которая описывает равновесное состояние для одного цикла (кругооборота) известного по К, Марксу воспроизводственного процесса действительной жизни общества; «Производство — Распределение – Обмен -Приобретение» (рис. 1, [2, с. 39]). Собственно балансовая матрица выделена тонированием соответствующих ячеек матричной таблицы.

Рис. 1. Балансовая матрица «производство — потребление», описывающая равновесное состояние общества (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов)
Как видно из схемы балансовой матрицы рисунка 1, это «условное общество» состоит из трёх агентов производителей (предприятий или коллективов, или лиц) и, с другой стороны, — одновременно состоит из тех же трёх агентов, но уже в ранге потребителей (предприятий, коллективов, или лиц). При этом за один цикл воспроизводственного оборота первый агент-производитель (i = 1) производит 6000 единиц (шт.) продукции с индексом j = 1, второй агент-производитель (i = 2) производит 9000 единиц (шт.) продукции с индексом j = 2, третий агент-производитель (i = 3) производит 12000 единиц (шт.) продукции с индексом j = 3.
При этом за этот же цикл воспроизводственного оборота, но уже в части потребления произведённых продуктов, первый агент (i = 1) как агент-потребитель (k = 1) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 1 таблицы рисунка 1.
Соответственно, см. балансовую матрицу рисунка 1, второйй агент (i = 2) как агент-потребитель (k = 2) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 2 таблицы рисунка 1.
Наконец, согласно балансовой матрице рисунка 1 третийй агент (i = 3) как агент-потребитель (k = 3) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 3 таблицы рисунка 1.
Очевидно, что объемы потребления представленных в матрице рисунка 1 агентов-потребителей одинаковы как в объёмах, так и в структурах потребления. Более того, в целом для этого общества объемы и структура производства продукции та же, что и объёмы и структура потребления. Очевидно, что в потреблении агенты-потребители равны и каждый потребляет (получает) одно и то же количество продуктов по объёму каждого наименования. Далее, обозначим через Pik (i = 1, 2, …, m; k = 1, 2, …, n) количество продукта в каждой ячейке матрицы, выделенной на рисунке 1 серым тонированием. Общепринято, что первый индекс указывает строку, а поэтому сохраним за первым индексом обозначение «i», то есть — обозначение агента-производителя (строка). Соответственно зададим обозначение второго индекса через «k» — обозначение агента-потребителя (столбец). В данном примере максимальные значения индексов «i», «k» соответственно равны — m = 3, n = 3.
Рассмотрим собственно саму балансовую матрицу равновесного состояния, которая в таблице рисунка 1 выделена серым тонированием и отдельно представлена на рисунке 2. На схеме балансовой матрицы рисунка 2[2, с. 40] объёмы продуктов вписаны с дополнительным указанием по каждому элементу условного обозначения соответствующего количества продукта в формате — Pik = ХХХХ.
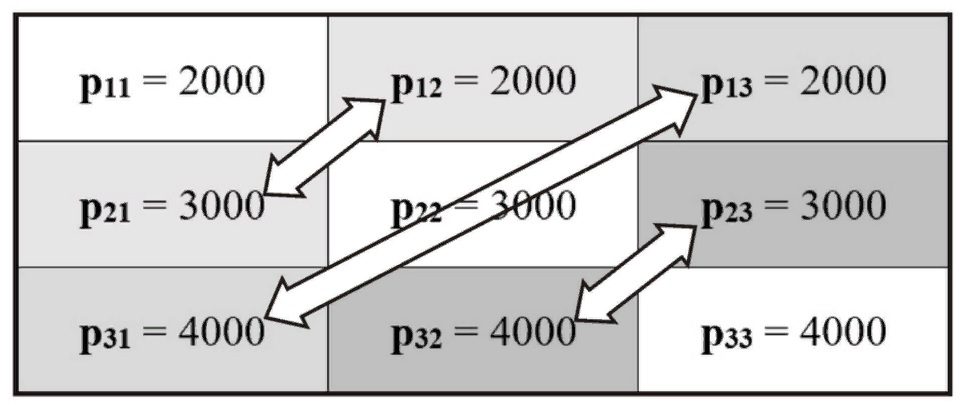
Рис. 2. Балансовая матрица «производство — потребление» в условиях равновесного состояния «условного общества»
Дополнительно на рисунке 2 двухсторонними фигурными стрелками соединены те элементы (ячейки) балансовой матрицы, агенты которых, как агенты-производители, вовлечены в «обмен», на что указывает особое положение соответствующей ячейки матрицы и её пара индексов «i» и «k» при Pik. При этом наблюдается «зеркальное» отображение индексов этих пар ячеек, точнее, индексов соответствующих объёмов производства (i) и потребления (k) для указываемых двухсторонней стрелкой пар объемов (колтчеств) различных продуктов — Pik = ХХХХ, например:
— левая короткая двухсторонняя стрелка (слева направо)
P21 = 3000 (i=2, k=1) и P12 = 2000 (i=1, k=2);
— средняя длинная двухсторонняя стрелка (слева направо)
P31 = 4000 (i=3, k=1) и P13 = 2000 (i=1, k=3);
— правая короткая двухсторонняя стрелка (слева направо)
P32 = 4000 (i=3, k=2) и P23 = 3000 (i=2, k=3);
Здесь «зеркальное отображение» двойных индексов представлено, образно говоря, тремя следующими их метаморфозами (>>> — знак метаморфозы зеркального отображения двойных индексов):
— левая короткая двухсторонняя стрелка (слева направо)
двойной индекс «21» (i=2, k=1) >>> «12» (i=1, k=2);
— средняя длинная двухсторонняя стрелка (слева направо)
двойной индекс «31» (i=3, k=1) >>> «13» (i=1, k=3);
— правая короткая двухсторонняя стрелка (слева направо)
двойной индекс «32» (i=3, k=2) >>> «23» (i=2, k=3).
Каждый из агентов выступает одновременно и как агент-производитель (первый индекс двойной индексации — i), отчуждающий свой продукт, и как агент-потребитель (второй индекс двойной индексации — k), приобретающий для своего потребления продукт другого вида «взамен» отчуждённого продукта. В результате такого взаимодействия осуществляется метаболический «обменный» процесс, который в буржуазном обществе, в случае, если типологии обеих продуктов «внешний предмет, вещь», принято именовать «товарообменом». Ячейки матрицы с элементами этих пар, дополнительно к двухсторонним стрелкам, выделены тонировкой различной интенсивности, одинаковой для каждой пары.
Так, например, пара элементов P12 = 2000 и P 21 = 3000? соединённых малой двухсторонней фигурной стрелкой и имеющих светло-серое тонирование соответствующих ячеек балансовой матрицы (см. рис.2), последовательно читается следующим образом:
— Первый агент с индексом i = 1 отчуждает в пользу второго агента с индексом k = 2 ровно 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблице рисунка 1 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом второй агент с индексом i = 2 отчуждает в пользу первого агента k = 1 ровно 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно той же матричной таблице рисунка 1 только второй агент производит продукты с индексом j = 2 (и только этот продукт).
Следующая пара элементов P13 = 2000 и P31 = 4000, соединённых длинной двухсторонней фигурной стрелкой (см. рис. 2), последовательно читается следующим образом:
— Первый агент с индексом i = 1 отчуждает в пользу третьего агента с индексом k = 3 ровно 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблице рисунка 1 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом третий агент i = 3 агент отчуждает в пользу первого агента k = 1 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблице рисунка 1 только третий агент производит продукты с индексом j = 3 (и только этот продукт).
Наконец, пара элементов P23 = 3000 и P32 = 4000, соединённых малой двухсторонней фигурной стрелкой и имеющих тёмное тонирование соответствующих ячеек балансовой матрицы (см. рис. 2), последовательно читается следующим образом:
— Второй агент с индексом i = 2 отчуждает в пользу третьего агента с индексом k = 3 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно матричной таблице рисунка 1 только второй агент производит продукты с индексом j = 2 (и только этот продукт). При этом третий агент i = 3 агент отчуждает в пользу второго агента k = 2 ровно 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблицы рисунка 1 только третий агент производит продукты с индексом j = 3 (и только этот продукт).
Таким образом имеем три «меновых» отношения для всех трёх продуктов производимых и потребляемых в рассматриваемом иллюстративном примере условного общества. Эти три меновых отношения представлены в таблице рисунка 3 [2, с. 43]
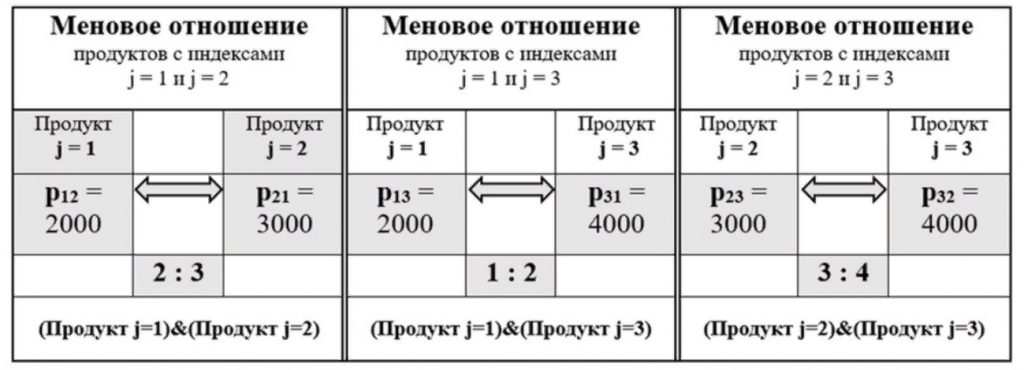
Рис. 3. Меновые отношения для всех трёх продуктов, производимых и потребляемых в рассматриваемом иллюстративном примере условного общества
Выполненный анализ условного примера формирования балансовой матрицы «производство — потребление» основан на учёте целостного единства воспроизводственного процесса действительной жизни общества, «единого целого» — по К. Марксу. Он, выполненный анализ, показал, что так называемое «меновое отношение» возникает НЕ на базе «меновой стоимости товаров», которая как утверждает автор «Капитала», — «и есть их стоимость».
В частности, К. Маркс так характеризует этот стоимостный остаток:
— «…одинаковой для всех призрачной предметности, простого сгустка лишенного различий человеческого труда, т. е. затраты человеческой рабочей силы безотносительно к форме этой затраты. Все эти вещи представляют собой теперь лишь выражения того, что в их производстве затрачена человеческая рабочая сила, накоплен человеческий труд. Как кристаллы этой общей им всем общественной субстанции, они суть стоимости — товарные стоимости.
…Таким образом, то общее, что выражается в меновом отношении, или меновой стоимости товаров, и есть их стоимость. Дальнейший ход исследования приведет нас опять к меновой стоимости как необходимому способу выражения, или форме проявления стоимости;…
…Как же измерять величину ее стоимости? Очевидно, количеством содержащегося в ней труда, этой «созидающей стоимость субстанции». Количество самого труда измеряется его продолжительностью, рабочим временем…» (Выделено мной. — ХАТ) [1, с. 4].
Однако, — базой возникновения менового отношения, как показывает приведённый условный пример одного цикла кругооборота (обращения) воспроизводственного процесса, является устойчивое сохранение равновесного состояния общества как единого целого, что «свойственно всякому органическому целому», «всем общественным субстанциям». При этом заметим отсутствие в приведённом анализе даже какого-либо упоминания стоимости, рабочего времени и «труда, этой «созидающей стоимость субстанции»» по Марксу.
Следовательно, можно полагать, утверждать, что полученные в приведённом примере меновые отношения есть выражение «органическим целым» общества его целостного единства. А это отторгает утверждение автора «Капитала» о стоимости, лежащей в основе менового отношения, — в основе этой, марксовой, «пропорции».
Так, в этой связи, изначально, К. Маркс пишет:
«Меновая стоимость прежде всего представляется в виде количественного соотношения, в виде пропорции, в которой потребительные стоимости одного рода обмениваются на потребительные стоимости другого рода, — случайного соотношения, постоянно изменяющегося в зависимости от времени и места. Меновая стоимость кажется поэтому чем-то случайным и чисто (совершенно — ХАТ) относительным, внутренняя для товара имманентная (присущая самому товару — ХАТ) меновая стоимость (valeur intrinsèque) представляет, по-видимому, бессмыслицу (представляется каким-то contradictio in adjecto [противоречием в определении] — ХАТ)» [1, с. 2].
Однако вместе с этим, выявленным нами отторжением стоимости, «обессмысливается» и такое заключение из политэкономии «Капитала»:
«Стоимость одного товара относится к стоимости каждого другого товара, как рабочее время, необходимое для производства первого, к рабочему времени, необходимому для производства второго. «Как стоимости, все товары суть лишь определенные количества застывшего рабочего времени»» [1, с. 5].
Наконец, как пишет К. Маркс, — «Если отвлечься от потребительной стоимости товарных тел, то у них остается лишь одно свойство, а именно то, что они — продукты труда» [1, с. 3].
Следует заметить, что этим отторгается, скорее — «ущемляется», и само понятие менового отношения, так как не только «продукты труда» охватываются меновым отношением. Это «отторжение и ущемление» по сути признаёт и сам К. Маркс, когда упоминает «товарную форму», так он пишет:
«Вещи, которые сами по себе не являются товарами, например, совесть, честь и т.д., могут стать продажными для своих владельцев и таким образом при посредстве цены приобрести товарную форму. Следовательно, вещь формально может иметь цену, не имея стоимости».
То есть, здесь, используя термин «товарная форма», К. Маркс признаёт возможность не только существования меновых отношений без стоимости, — «не имея стоимости», но и существование «вещей» и продуктов в меновых отношениях без «застывшего рабочего времени».
Следовательно, изложенный балансовый метод матричного анализа меновых отношений, является достаточно универсальным в анализе меновых и трудовых отношений в действительной жизни общества, в анализе социального метаболизма современного общества.
ЛИТЕРАТУРА
1.Маркс К. Капитал, Критика политической экономии. Т. 1. Книга 1. М.-Л.: Государственное издательство, 1929.
2.Харчевников А. Т. Социальный метаболизм. Полилогический матричный анализ «обменных процессов и стоимости. Издательские решения Ridero? 2021.

